Основной закон релятивистской динамики: 21. Основной закон релятивистской динамики. – Релятивистская механика — Википедия
21. Основной закон релятивистской динамики.
Основные кинематические характеристики поступательного движения.
Поступательное движение– это такое движение, при котором любая прямая, связанная с движущимся телом, остаётся параллельной самой себе.
Путь– это длинна участка траектории с момента начала отсчёта времени и до окончания.
Перемещение– это вектор, проведенный из начального положения в конечное положение в данный момент времени.
Скорость – величина, которая вводится для характеристики движения материальной точки. Бывает средняя и мгновенная.
Ускорение— это векторная величина, определяемая первой производной скорости по времени.
Нормальное и тангенциальное ускорения.
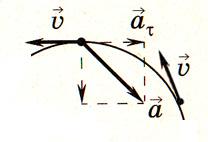
При криволинейном движении скорость направлена по касательной к траектории. Поскольку направление скорости постоянно изменяется, то криволинейное движение — всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным |
|
В общем
случае ускорение направлено под углом
к скорости. Составляющая ускорения,
направленная вдоль скорости,
называется тангенциальным
ускорением | |
| |
Составляющая ускорения, направленная
к центру кривизны траектории, т.е.
перпендикулярно (нормально) скорости,
называется нормальным ускорением | |
| |
Здесь R — радиус кривизны траектории в данной точке. |
Определение пути при различных видах движения.
При равномерном движении тела путь описывается формулой S=v*t
При равнопеременном движении тела путь
описывается формулой 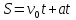
При переменном движении тела путь описывается S=f(t)
Кинематические характеристики вращательного движения.
Вращательное движение– это такое движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, которая называется осью вращения.
Угловая скорость– векторная
величина, равная первой производной
угла поворота по времени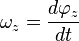 ,
,
Угловое ускорение— векторная
физическая величина, характеризующая
быстроту изменения угловой скорости
твёрдого тела. Угловое ускорение равно
первой производной от угловой скорости
по времени. Формула угловой скорости: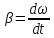
Связь между кинематическими характеристиками поступательного и вращательного движения.
Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость v и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение j, угловая скорость w и угловое ускорение a (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками:
перемещение
s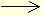 угловое
перемещение j = s/R;
скорость vугловая
скорость w = v/R;
ускорение a
угловое
перемещение j = s/R;
скорость vугловая
скорость w = v/R;
ускорение a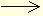 угловое
ускорение a = a/R.
угловое
ускорение a = a/R.
Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:
s
= vt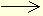 j
= wt,
v = v0 +
at
j
= wt,
v = v0 +
at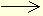
Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор R, проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела v, направленному по касательной к окружности в этой точке. Определим вектор w, который по модулю равен угловой скорости w и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора w. Тогда связь трех взаимно перпендикулярных векторов R, v и w можно записать с помощью векторного произведения векторов:
v = wR.
Масса и импульс. Современная трактовка законов Ньютона.
Масса –1) мера инертности тела.
2) мера гравитационного взаимодействия.
3)
мера энергии тела. E=m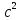
4) мера количества вещ-ва. m=pV
Импульс (Количество
движения) — векторная физическая
величина, являющаяся
мерой
 .
.
Первый закон Ньютона:
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Второй закон Ньютона:
В
инерциальной системе отсчёта ускорение,
которое получает материальная точка,
прямо пропорционально равнодействующей
всех приложенных к ней сил и обратно
пропорционально её массе.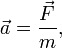
Третий закон Ньютона:
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
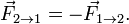
Второй закон Ньютона как уравнение движения. Сила как производная импульса.
Второй закон механики гласит: произведение массы тела на его ускорение равно действующей силе, а направление ускорения совпадает с направлением силы. Такова его современная формулировка. Ньютон сформулировал его иначе: изменение количества движения пропорционально приложенной действующей силе и происходит по направлению той прямой, по которой эта сила действует. Т.е. Ньютон в формулировке второго закона оперирует понятием количества движения, понимаемым как мера движения, пропорциональная массе и скорости. Количество движения – величина векторная (Ньютон учитывал направление движения при формулировании правила параллелограмма скоростей).Но это понятие в истории науки не удержалось (и сейчас заменено понятием импульса), поскольку было неясно, чем измерять движение.
Второй закон Ньютона — ускорение, приобретаемое материальной точкой, пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
a = F/m
Эта формула выражает основной закон движения.
Более общая формулировка второго закона Ньютона – скорость изменения импульса материальной точки равна действующей на нее силе.
F = d p/dt
Третий закон Ньютона и закон сохранения импульса.
Закон сохранения импульса гласит, что суммарный импульс изолированной системы не изменяется со временем.
Принцип относительности Галилея.
Принцип относительности Галилея — принцип физического равноправия инерциальных систем отсчёта в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы. Отсюда следует, что никакими механическими опытами, проводящимися в какой-либо инерциальной системе, нельзя определить, покоится ли данная система или движется равномерно и прямолинейно.
Работа и кинетическая энергия. Мощность.
Механическая работа– физическая величина, определяющаяся произведением силы вдоль направления перемещения на пройденный путь.

Кинетическая энергия – физическая величина, равная половине произведения массы тела на квадрат его скорости.
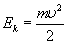
МощностьюP называется отношение произвольной
работыWк времени t, в
течение которого совершается работа.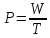
Консервативные и диссипативные силы.
В физике консервативные силы(потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Диссипативные силы— силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту.
Потенциальная энергия во внешнем поле сил. Понятие о градиенте. Потенциальная энергия взаимодействия.
Закон сохранения энергии в механике.

Таким
образом, в
изолированной системе, в которой
действуют консервативные силы,
механическая энергия сохраняется.
В этом состоит закон
сохранения механической энергии.
Энергия не создается и не уничтожается,
а только превращается из одной формы в
другую: из кинетической в потенциальную
и наоборот.
Учитывая, что в рассматриваемом конкретном
случае 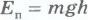 и
и 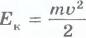 ,
можно закон сохранения механической
энергии записать так:
,
можно закон сохранения механической
энергии записать так:
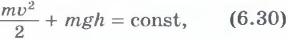
или
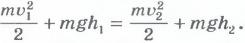
Закон сохранения импульса.
Импульсом называют векторную величину, равную произведению массы тела на ее скорость:
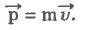
При взаимодействии тел замкнутой системы полный импульс системы остается неизменным:
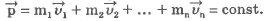
Закон сохранения импульса есть следствие второго и третьего законов Ньютона. Пример использования закона сохранения импульса.
Момент силы. Уравнение движения твердого тела.
Момент силы
– физическая величина, равная векторному
произведению радиус-вектора, (проведенного
от оси вращения к точке приложения силы
— по определению), на вектор этой силы. 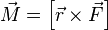
Момент инерции тела относительно оси. Теорема Штейнера.
Величина, численно равная произведению
массы материальной точки на квадрат
расстояния от оси вращения называют
моментом инерции материальной точки. 
Теорема Штейнера позволяет определить
момент инерции тела относительно
произвольной оси. 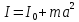 , где а – расстояние между данной осью
и параллельной осью, проходящей через
центр масс.
, где а – расстояние между данной осью
и параллельной осью, проходящей через
центр масс.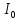 –
момент инерции данного тела.
–
момент инерции данного тела.
Описание | Положение оси a | Момент инерции Ja | |
| Материальная точка массы m | На расстоянии r от точки, неподвижная |
|
| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра |
|
| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра |
|
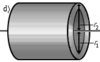
| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра |
|
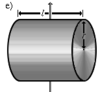
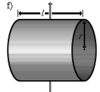
| Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс |
|
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс |
|
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс |
|
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец |
|
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы |
|
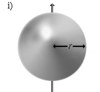
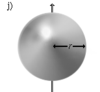
| Шар радиуса r и массы m | Ось проходит через центр шара |
|
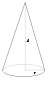
| Конус радиуса r и массы m | Ось конуса |
|
Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину |
| |
Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс |
| |
Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс |
| |
Момент импульса. Закон сохранения импульса. Энергия вращения тела.
Момент импульса— характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
L=const.
Закон сохранения момента импульса гласит, что он сохраняется в замкнутой системе.
Свободные оси. Гироскопы.
Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела).
Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения тела.
Вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым.
Гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью.
Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот) и т. д. При всяком отклонении от курса вследствие каких-то воздействий (волны, порыва ветра и т. д.) положение оси гироскопа в пространстве сохраняется.
Специальная теория относительности. Преобразования Лоренца и следствия из них.
Специальная теория относительности(СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.
Интервал. Релятивистский закон сложения скоростей.
Пусть интервал времени между двумя событиями, происходящими в одной и той же точке инерциальной системы К, равен 0. Этими событиями, например, могут быть два удара метронома, отсчитывающего секунды.
Тогда
интервал между
этими же событиями в системе отсчета K1,
движущейся относительно системы К со
скоростью 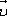 ,
выражается так:
,
выражается так:
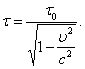 (2.2)
(2.2)
Очевидно, что > 0. В этом состоит релятивистский эффект замедления времени в движущихся системах отсчета.
Если <<с,
то в формулах (2.1) и (2.2) можно пренебречь
величиной 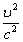 .
Тогдаll0 и 0,
т. е. релятивистское сокращение размеров
тел и замедление времени в движущейся
системе отсчета можно не учитывать.
.
Тогдаll0 и 0,
т. е. релятивистское сокращение размеров
тел и замедление времени в движущейся
системе отсчета можно не учитывать.
Релятивистский закон сложения скоростей
Новым релятивистским представлениям о пространстве и времени соответствует новый закон сложения скоростей. Очевидно, что классический закон сложения скоростей не может быть справедлив, так как он противоречит утверждению о постоянстве скорости света в вакууме.
Если
поезд движется со скоростью 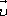 и
в вагоне в направлении движения поезда
распространяется световая волна, то ее
скорость относительно Земли должна
равняться опять-таки
и
в вагоне в направлении движения поезда
распространяется световая волна, то ее
скорость относительно Земли должна
равняться опять-таки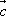 ,
а не
,
а не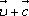 .
Новый закон сложения скоростей и должен
приводить к требуемому результату.
.
Новый закон сложения скоростей и должен
приводить к требуемому результату.
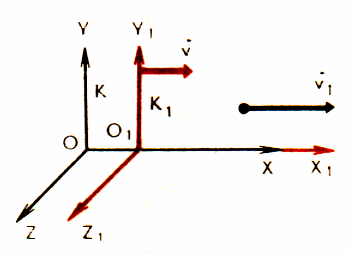
Мы
запишем закон сложения скоростей для
частного случая, когда тело движется
вдоль оси Х1 системы
отсчета К1,
которая в свою очередь движется со
скоростью 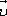 относительно
системы отсчетаК.
Причем в процессе движения координатные
оси Х и Х1 все
время совпадают, а координатные
оси Y и Y1, Z и Z1 остаются
параллельными (рис. 42).
относительно
системы отсчетаК.
Причем в процессе движения координатные
оси Х и Х1 все
время совпадают, а координатные
оси Y и Y1, Z и Z1 остаются
параллельными (рис. 42).
|
|
|
Рис. 42
Обозначим скорость тела относительно К1 через 1, а скорость этого же тела относительно К через 2. Тогда релятивистский закон сложения скоростей будет иметь вид
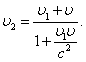 (2.3)
(2.3)
Если <<с и 1<<с,
то членом 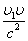 в
знаменателе можно пренебречь, и вместо
(2.3) получим классический закон сложения
скоростей:2=1+.
в
знаменателе можно пренебречь, и вместо
(2.3) получим классический закон сложения
скоростей:2=1+.
При 1=с скорость 2 также равна с, как этого требует второй постулат теории относительности. Действительно,
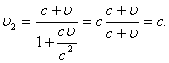
Замечательным свойством релятивистского закона сложения скоростей является то, что при любых скоростях 1 и (конечно, не больших с) результирующая скорость 2 не превышает с.
Масса движущихся релятивистских частиц зависит от их скорости:
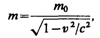 (39.1)
(39.1)
где m0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
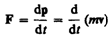
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
Основной закон релятивистской динамики материальной точки имеет вид
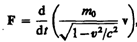
или
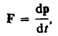
где
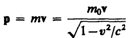
— релятивистский импульс материальной точки.
22. Закон взаимосвязи массы и энергии покоя.
– любое тело обладает энергией уже только благодаря факту своего существования, и эта энергия, называемая собственной энергией тела, равна произведению массы тела на квадрат скорости света в вакууме. Собственную энергию тела иначе называют энергией покоя. В нее не входят ни кинетическая энергия тела, ни его потенциальная энергия во внешнем поле. Из закона взаимосвязи массы и энергии следует, что если покоящемуся телу сообщить некоторую энергию, то его масса изменится. Однако в обычных макроскопических процессах, с которыми мы имеем дело в жизни и технике, изменения массы, обусловленные изменением энергии тел, чрезвычайно малы. Так, при нагревании одного литра воды от 0 до 100 °С масса воды увеличивается всего лишь на 5×10–9 грамма. Но, например, масса Солнца из-за потерь энергии на излучение ежесекундно уменьшается более чем на 4 миллиона тонн.
23. Частицы с нулевой массой.
24. Модель идеального газа. Уравнение состояния.
Модель идеального газа удовлетворяет след. Условиям:
Собственный объём молекул газа пренебрежимо малы по сравнению с объёмом сосуда.
Столкновения молекул газа между собой и стенками сосуда абсолютно упругие.
Между молекулами притяжение сведено к минимуму.
Модель
идеального газа удовлетворяет уравнению
Менделеева-Клапейрона 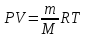
25. Основное уравнение мкт газов.
Основное
уравнение МКТ: 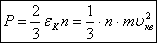 где—
средняя кинетическая энергия
поступательного движения одной
молекулы,
где—
средняя кинетическая энергия
поступательного движения одной
молекулы, —
концентрация молекул,
—
концентрация молекул,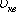 —
средняя квадратичная скорость.,
—
средняя квадратичная скорость.,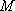 —
молярная масса газа,
—
молярная масса газа,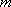 —
масса одной молекулы.
—
масса одной молекулы.
Число
ударов молекул о стенку при условии,
что скорости частиц одинаковы и
равновероятно распределены по шести
направлениям: вперед — назад, налево —
направо, вверх – вниз: 
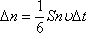 При
ударе одной частицы о стенку, частица
передает стенке удвоенный импульс.
Суммарный импульс, которые частицы
передают стенке:
При
ударе одной частицы о стенку, частица
передает стенке удвоенный импульс.
Суммарный импульс, которые частицы
передают стенке: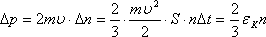 ,
где
,
где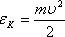 —
средняя кинетическая энергия
поступательного движения одной
молекулы.
Давление газа равно импульсу,
которые частицы при ударах передают
стенке за единицу времени на единицу
поверхности:
—
средняя кинетическая энергия
поступательного движения одной
молекулы.
Давление газа равно импульсу,
которые частицы при ударах передают
стенке за единицу времени на единицу
поверхности: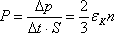 .
.
Релятивистская механика — Википедия
Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.
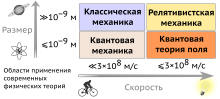 Область применения релятивистской механики
Область применения релятивистской механикиВ классической механике пространственные координаты и время являются независимыми (при отсутствии голономных связей, зависящих от времени), время является абсолютным, то есть течёт одинаково во всех системах отсчёта, и действуют преобразования Галилея. В релятивистской же механике события происходят в четырёхмерном пространстве, объединяющем физическое трёхмерное пространство и время (пространство Минковского) и действуют преобразования Лоренца. Таким образом, в отличие от классической механики, одновременность событий зависит от выбора системы отсчёта.
Основные законы релятивистской механики — релятивистское обобщение второго закона Ньютона и релятивистский закон сохранения энергии-импульса — являются следствием такого «смешения» пространственных и временной координат при преобразованиях Лоренца.
Сила определяется как
- F→=dp→dt.{\displaystyle {\vec {F}}={\frac {d{\vec {p}}}{dt}}.}
Также известно выражение для релятивистского импульса:
- p→=mv→1−v2/c2.{\displaystyle {\vec {p}}={\frac {m{\vec {v}}}{\sqrt {1-v^{2}/c^{2}}}}.}
Взяв для определения силы производную по времени от последнего выражения, получим:
- dp→dt=mγa→+mγ3β→(β→a→),{\displaystyle {\frac {d{\vec {p}}}{dt}}=m\gamma {\vec {a}}+m\gamma ^{3}{\vec {\beta }}({\vec {\beta }}{\vec {a}}),}
где введены обозначения: β→≡v→c{\displaystyle {\vec {\beta }}\equiv {\frac {\vec {v}}{c}}} и γ≡11−v2/c2{\displaystyle \gamma \equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}}.
В результате выражение для силы приобретает вид:
- F→=mγa→+mγ3β→(β→a→).{\displaystyle {\vec {F}}=m\gamma {\vec {a}}+m\gamma ^{3}{\vec {\beta }}({\vec {\beta }}{\vec {a}}).}
Отсюда видно, что в релятивистской механике в отличие от нерелятивистского случая ускорение не обязательно направлено по силе, в общем случае ускорение имеет также и составляющую, направленную по скорости.
Запишем интеграл действия, исходя из принципа наименьшего действия
- S=−∫abαds,{\displaystyle S=-\int \limits _{a}^{b}\alpha ds,}
где α{\displaystyle \alpha }-положительное число. Как известно из специальной теории относительности (СТО)
- ds=c1−v2/c2dt.{\displaystyle ds=c{\sqrt {1-v^{2}/c^{2}}}dt.}
Подставляя в интеграл движения, находим
- S=−∫t1t2αc1−v2/c2dt.{\displaystyle S=-\int \limits _{t_{1}}^{t_{2}}\alpha c{\sqrt {1-v^{2}/c^{2}}}dt.}
Но, с другой стороны, интеграл движения, можно выразить через функцию Лагранжа
- S=∫t1t2Ldt.{\displaystyle S=\int \limits _{t_{1}}^{t_{2}}{\mathcal {L}}dt.}
Сравнивая последние два выражения, нетрудно понять, что подынтегральные выражения должны быть равны, то есть
- L=−αc1−v2/c2.{\displaystyle {\mathcal {L}}=-\alpha c{\sqrt {1-v^{2}/c^{2}}}.}
Далее, разложим последнее выражение по степеням vc{\displaystyle {\frac {v}{c}}}, получим
- L≃αc+αv22c.{\displaystyle {\mathcal {L}}\simeq \alpha c+{\frac {\alpha v^{2}}{2c}}.}
Первый член разложения не зависит от скорости, а значит не вносит никаких изменений в уравнения движения. Тогда, сравнивая с классическим выражением функции Лагранжа: mv22{\displaystyle {\frac {mv^{2}}{2}}}, нетрудно определить константу α{\displaystyle \alpha }
- α=mc.{\displaystyle \alpha =mc.}
Таким образом, окончательно получаем вид функции Лагранжа свободной частицы
- L=−mc21−v2/c2.{\displaystyle {\mathcal {L}}=-mc^{2}{\sqrt {1-v^{2}/c^{2}}}.}
Рассуждения, приведенные выше, можно рассматривать не только для частицы, но и для произвольного тела, лишь бы его части двигались как одно целое.
Поскольку квадрат 4-вектора импульса Pα{\displaystyle P_{\alpha }} является постоянной величиной:
- PαPα−m2c2=0,{\displaystyle P_{\alpha }P^{\alpha }-m^{2}c^{2}=0,}
то релятивистская частица может рассматриваться как механическая система с неголономной связью в 4-мерном псевдоевклидовом пространстве[1][2][3].
Основной закон релятивистской динамики.
Масса движущихся релятивистских частиц зависит от их скорости:
(39.1)
где m0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
Основной закон релятивистской динамики материальной точки имеет вид
или
где
— релятивистский импульс материальной точки.
Найдем кинетическую энергию релятивистской частицы. Раньше было показано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:
(6.1)
Учитывая, что , и подставив в (6.1) выражение (5.2), получаем
.
Преобразовав данное выражение с учетом того, что , и формулы (6.1), придем к выражению
, (6.2)
т. е. приращение кинетической энергии частицы пропорционально приращению ее массы.
Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя , то, проинтегрировав (6.2), получим
, (6.3)
или кинетическая энергия релятивистской частицы имеет вид
. (6.4)
Выражение (6.4) при скоростях переходит в классическое:
(разлагая в ряд при , правомерно пренебречь членами второго порядка малости).
А.Эйнштейн обобщил положение (6.2), предположив, что оно справедливо не только для кинетической энергии частицы, но и для полной энергии, а именно любое изменение массы сопровождается изменением полной энергии частицы,
. (6.5)
Отсюда А.Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:
. (6.6)
Уравнение (6.6), равно как и (6.5), выражает фундаментальный закон природы – закон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле. Закон (6.6) можно, учитывая выражение (6.3), записать в виде
,
откуда следует, что покоящееся тело (Ек=0) также обладает энергией
,
называемой энергией покоя.В классической механике энергия покоя Е0не учитывается, считая, что при энергия покоящегося тела равна нулю.
В силу однородности временив релятивистской механике, как и в классической, выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Из формул (6.6) и (5.4) найдем релятивистское соотношение между полной энергией и импульсом частицы:
. (6.7)
Возвращаясь к уравнению (6.6), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко всем формам энергии, т. е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса
(6.8)
и, наоборот, со всякой массой связана энергия (6.6).
Чтобы охарактеризовать прочность связи и устойчивость системы каких-либо частиц (например, атомного ядра как системы из протонов и нейтронов), вводят понятие энергии связи. Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро – на протоны и нейтроны). Энергия связи системы
. (6.9)
где m0i – масса покоя i-й частицы в свободном состоянии; М0 – масса покоя системы, состоящей из п частиц.
Закон взаимосвязи (пропорциональности) массы и энергии блестяще подтвержден экспериментом о выделении энергии при протекании ядерных реакций. Он широко используется для расчета энергетических эффектов при ядерных реакциях и превращениях элементарных частиц.
Рассматривая выводы специальной теории относительности, видим, что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений. Масса тела не остается постоянной величиной, а зависит от скорости тела; длина тел и длительность событий не являются абсолютными величинами, а носят относительный характер; наконец, масса и энергия оказались связанными друг с другом, хотя они и являются качественно различными свойствами материи.
Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи – пространство-время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Элементы релятивисткой динамики
Принцип относительности Эйнштейна утверждает инвариантность всех законов природы по отношению к переходу от одной инерциальной системе отсчета к другой. Отсюда следует, что уравнения, которые описывают законы природы, должны быть инвариантны относительно преобразований Лоренца.
Импульс. Релятивистская масса
Во время создания СТО теории, удовлетворяющей данному условию, она подразумевала уже существующую теорию электродинамики Максвелла. Уравнения вышли неинвариантными относительно преобразований Лоренца, что требовало пересмотра и уточнения законов механики.
Для этого Эйнштейн основывался на требованиях выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Чтобы он выполнялся во всех инерционных системах отсчета, следовало изменить определение импульса тела.
Определение 1Классический импульс p→=mν→ заменяют релятивистским p→ с массой m и скоростью движения ν→. Запись принимает вид:
p→=mν→1-ν2c2=mν→1-β2.
Если данное определение задействовать при решении, то закон сохранения суммарного импульса частиц выполнится во всех инерциальных системах, в которых есть связь с преобразованиями Лоренца. Когда β→0 релятивистский импульс перейдет в классический.
Определение 2Масса m считается фундаментальной характеристикой частицы. Она не зависит от выбора инерциальной системы отсчета, скорости движения.
Некоторые учебники трактуют это как массу покоя, обозначаемую m0. Позже вводилась релятивистская масса частицы m01-β2, которая зависела от скорости движения частицы. Современная физика отказывается от данных терминологий.
Определение 3Запись основного закона релятивистской динамики материальной точки принимает вид, аналогичный второму закону Ньютона:
F→=dp→dt,
тогда p→ примет значение релятивистского импульса частицы. Отсюда следует
F→=ddtmv→1-ν2c2.
Скорость частицы в релятивистской механике не пропорциональна релятивистскому импульсу, то есть скорос

ТОП 10: |
⇐ ПредыдущаяСтр 25 из 30Следующая ⇒ Масса движущихся релятивистских частиц зависит от их скорости:
где m0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса. Основной закон релятивистской динамики материальной точки имеет вид
или
где
— релятивистский импульс материальной точки. Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой. В силу однородности пространства в релятивистской механике выполняетсязакон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выражение для импульса. Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально переход осуществляется при с®¥). Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме). Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем будет показано, что на основании этой зависимости производятся расчеты ускорителей. Вопрос 41.1 Закон взаимосвязи массы и энергии
Вопрос 41.2 |
§ 39. Основной закон релятивистской динамики материальной точки
Масса движущихся релятивистских частиц зависит от их скорости:
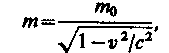 (39.1)
(39.1)
где т0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Из принципа относительности Эйнштейна (см. § 35), утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
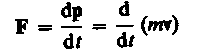
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса. Основной закон релятивистской динамики материальной точки имеет вид
или
где
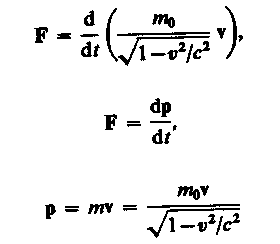
— релятивистский импульс материальной точки.
Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.
В силу однородности пространства (см. § 9) в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выражение для импульса.
Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v«c. Законы классической механики получаются как следствие теории относительности для предельного случая v«c (формально пере ход осуществляется при с ). Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем (см. § 116) будет показано, что на основании этой зависимости производятся расчеты ускорителей.
• Как определяется интервал между событиями? Доказать, что он является инвариантом при переходе от одной инерциальной системы отсчета к другой.
•Какой вид имеет основной закон релятивистской динамики? Чем он отличается от основного закона ньютоновской механики?
В чем заключается закон сохранения релятивистского импульса?
§ 39. Основной закон релятивистской динамики материальной точки
Масса движущихся релятивистских частиц зависит от их скорости:
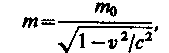 (39.1)
(39.1)
где т0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Из принципа относительности Эйнштейна (см. § 35), утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
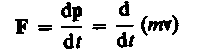
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса. Основной закон релятивистской динамики материальной точки имеет вид
или
где
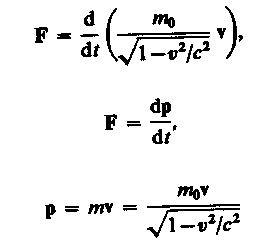
— релятивистский импульс материальной точки.
Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.
В силу однородности пространства (см. § 9) в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выражение для импульса.
Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v«c. Законы классической механики получаются как следствие теории относительности для предельного случая v«c (формально пере ход осуществляется при с ). Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем (см. § 116) будет показано, что на основании этой зависимости производятся расчеты ускорителей.
• Как определяется интервал между событиями? Доказать, что он является инвариантом при переходе от одной инерциальной системы отсчета к другой.
•Какой вид имеет основной закон релятивистской динамики? Чем он отличается от основного закона ньютоновской механики?
В чем заключается закон сохранения релятивистского импульса?

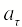
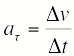
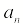
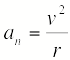

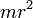

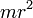

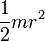
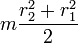
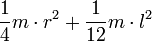


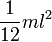

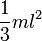
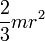

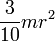
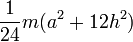
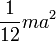
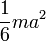
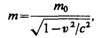 (39.1)
(39.1)
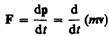
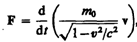 (39.2)
(39.2)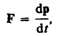 (39.3)
(39.3)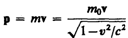 (39.4)
(39.4)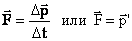
 Следовательно,
Следовательно, 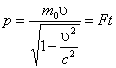 .
При υ=c получим, что со скоростью, равной скорости света может двигаться только тело, имеющее массу, равную нулю. Это говорит о предельном характере скорости света для материальных тел.
.
При υ=c получим, что со скоростью, равной скорости света может двигаться только тело, имеющее массу, равную нулю. Это говорит о предельном характере скорости света для материальных тел.
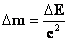 . Всякое изменение любой энергии (тела, частицы, системы тел) на
. Всякое изменение любой энергии (тела, частицы, системы тел) на 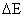 сопровождается пропорциональным изменением массы на Δm.
Нельзя говорить, что при этом масса переходит в энергию. В действительностиэнергия переходит из одной формы (механической) в другие (электромагнитную и ядерную), но любое превращение энергии сопровождается превращением массы.
сопровождается пропорциональным изменением массы на Δm.
Нельзя говорить, что при этом масса переходит в энергию. В действительностиэнергия переходит из одной формы (механической) в другие (электромагнитную и ядерную), но любое превращение энергии сопровождается превращением массы.